This article throws light upon the top seven investment criteria of capital budgeting. The investment criteria are: 1. Accounting or Average Rate of Return Method 2. Pay Back Period 3. Discounted Cash Flow Techniques 4. Net Present Value Method 5. Internal Rate of Return or Yield Method 6. Profitability Index (PI) or Benefit Cost Ratio 7. Terminal Value (TV) Method.
Investment Criteria of Capital Budgeting:
- Accounting or Average Rate of Return Method
- Pay Back Period
- Discounted Cash Flow Techniques
- Net Present Value Method
- Internal Rate of Return or Yield Method
- Profitability Index (PI) or Benefit Cost Ratio
- Terminal Value (TV) Method
Capital Budgeting: Investment Criteria #
1.
Accounting or Average Rate of Return Method:
The Average Rate of Return (ARR) method is used in order to measure the profit-abilities of the investment proposals. This is practically an accounting method and it incorporates the expected return which may be obtained from the project. Under this method average annual profit (after tax) is expressed as percentage of investment.
ADVERTISEMENTS:
There are a number of alternatives for calculating ARR. Although, there is no unanimity regarding its definition, the most common usage of the ARR which is found out by dividing the average annual profit / income after tax by the average investment.
In this connection, it may be noted that the average investment must be equal to the original investment plus salvage value, if any, divided by two. Moreover, the ARR can also be found out by dividing the total book value of investment (after depreciation) by the life of the project.
Therefore, this is nothing but an average rate which is expressed as a percentage and can be determined with the help of the following:
ARR = (Average Annual Profit after Tax/Average Investment) × 100
ADVERTISEMENTS:
Under this method, the investment which will give the highest rate of return will be accepted. Sometimes, a firm may fix a standard rate or cut-off rate of return and as such, investments which will not produce this rate will be excluded.
Illustration:
A Ltd. wants to purchase a machine. Two machines, viz. X and Y, are available in the market. The cost of each machine is Rs. 1,00,000. Their expected lives are 5 years.
Net profits before tax during the expected life of the machines are given below:

From the above information, ascertain which one is more profitable.
Solution:
Hence, Machine Y is more profitable since it gives the higher return.
ADVERTISEMENTS:
Illustration:
Determine the average rate of return from the following data of two machines A and B.
Solution:
Alternative approach:
Instead of taking the average cost of the project, the original cost is considered
In that case, the ARR, in case of both machines, will be {Rs. 7,375/Rs 56.125× 100} 13.14%
Advantages of ARR:
ADVERTISEMENTS:
(i) It is very simple and easy to calculate
(ii) It supplies the readily available accounting information.
Disadvantages of ARR:
(i) The significant demerits of this method is that it does not recognise the timings of cash inflows and outflows since it is based on accounting income instead of cash flows.
ADVERTISEMENTS:
(ii) Moreover, competing projects generally have a varying length of life. In order to find out the average earnings, additional years’ earnings of a project which has a longer life are compared with the earnings of a project which has a comparatively short life. This is unfair. As such, that system will be taken into consideration which will satisfy both the factors, viz. timing of income and varying length of life.
Additional Rate of Return:
It is the average additional profit expressed as percentage of investment. Under the circumstances, if it is found that the return is satisfactory in comparison with what is available, the replacement may be made. Before discussing the principles, it becomes necessary to explain the related terms in this respect, viz. (a) Investment, and (b) Average Additional profit.
(a) Investment:
(i) The original cost of investment;
(ii) Average Investment.
ADVERTISEMENTS:
We know that the original cost of an asset gradually diminishes from year to year over its effective life since the capital cost is recovered by way of depreciation charges. As such, if the straight line method of depreciation is followed, the average investment will be the half of the depreciable part plus the whole of the non-depreciable (remaining) part of the cost of the investment.
It should be mentioned that the depreciation portion is divided by two since the uncovered investment declines from the original cost of the asset to zero.
Illustration:
Find out the Average Investment.
Solution:
Average Investment = Rs. 20,000 – Rs. 5,000/2 + Rs. 5,000
= Rs. 12.500
(b) Average additional profit:
It is simply the difference between the profit which arises out of the sales proceeds of output produced by the new machine and those which are produced by the machine which is proposed to be replaced. It may be taken (for the purpose of calculating return on investment) as the profit either before-tax or after-tax.
Illustration:
ABC Co. has a machine which has been in operation for 6 years. The management is considering a proposal to purchase an improved model of a similar machine which gives an increased output Give your opinion as a Cost Accountant in regard to the proposal from the following data:
Solution:
Before taking up the actual decisions we are to compare the profitability statement of both the machines which are computed as under:
Hence, if the proposed project is undertaken, there will be an additional return on capital invested @ 27.5% before tax and 13.75% after tax, which may be considered as satisfactory. Therefore, the new project may be taken into consideration.
Acceptance Rule:
From the foregoing discussion it becomes clear that the financial decision-maker can decide whether a particular project will be undertaken or not with the help of the ARR, i.e. whether a project will be accepted or whether the same will be rejected. The accept-reject criterion, on the basis of the ARR, is followed by the management.
In other words, those projects will be accepted whose ARR, is higher than the minimum established rate/standard rate and those projects will be rejected whose ARR is less than the said minimum established rate/standard rate. Ranking method may also be used here. That project will be given rank one which has highest ARR and on the contrary lowest rank will be assigned if the ARR is lowest.
Evaluation of ARR:
Before evaluating ARR, its merits and drawbacks should carefully be considered. Its advantages are given below:
(i) The most significant attribute of ARR is that it is very simple to understand and easy to calculate.
(ii) It can be easily computed on the basis of accounting data which are furnished by the financial statements.
(iii) It recognises the entire stream of income while calculating the accounting rate.
The ARR is not even free from snags. They are discussed below:
(i) The principal shortcoming of ARR is that it recognises only the accounting income instead of cash flows.
(ii) It does not recognise the time value of money.
(iii) It does not take into consideration the length of lives of the projects.
(iv) It does not consider the fact that the profits may be re-invested.
Capital Budgeting: Investment Criteria #
2.
Pay Back Period:
The Pay Back Period Method is the second unsophisticated method of capital budgeting and is widely employed in order to overcome some of the shortcomings of ARR method It recognises that recovery of the original investment is an important element while appraising capital expenditure decisions.
It may be stated that it is simply an application of ‘break-even’ concept to investment. Practically, this method gives the answer about the question, ‘How many years will it take for the cash benefits to pay the original cost of an investment?
It is defined as the number of years required to cover the original cash outlay which are invested in a project. In other words, Pay Back Period is the period required for the savings in costs or net cash flow after tax but before depreciation, to recover the cost of investment.’
Thus, Pay Back Period is computed when:
(i) Cash flow accrues at even rate, i.e. where there is equal cash inflow:
Pay Back Period (P.B P.) = Cost of the investment Cash outlay/ Annual Vet Cash Inflow
(ii) Where there is unequal cash inflow:
The P B P. can be found out by adding up the cash inflows until the total is equal to the initial cash investment.
Illustration:
(Where there is equal cash inflow):
A project requires an investment of Rs. 1.00.000 with a life of 10 years which yield an expected annual net cash inflow of Rs. 25.000 Compute the pay-back period.
Solution:
Pay Back Period (P.B P.) = Cost of the investment (projects)/ Annual Net Cash Inflow
= Rs. 1,00,000 / Rs. 25,000 = 4 years.
Illustration:
(Where there is unequal cash inflow):
Calculate the payback period for a project which requires a cash outlay of Rs. 40,000 but the same generates a cash inflow of Rs. 16,000; Rs 12,000; Rs 10,000 and Rs. 6,000
Solution:
If we add the cash inflows for the first year, we find that Rs. 38,000 is recovered against the total cash outlay of Rs 40,000 leaving an unrecovered part of Rs. 2,000. But in the fourth year generation of cash inflow are Rs 6,000 and over Rs 2,000 of the original outlay remains to be recovered.
If cash inflows occur at an even rate during the year, the time required to cover Rs. 2,000 will be (Rs 2.000/Rs 6.000 × 12) 4 months. Thus, the Pay Back Period is 3 years plus 4 months.
Under the Pay Back Period Method, the time period which is necessary in order to recover its capital cost is calculated and that project will be treated as best which will take the shortest pay-back period. This principal is based on the understanding that the original outlay must be returned if the enterprise continues its operation.
It should be remembered that if the estimated productive period does not exceed the estimated pay-back period, a part of the invested capital may be lost and hence such project is rejected This method is particularly applicable where (i) the cost of the project is comparatively small and which is completed in a short period, (ii) the project is productive immediately after the investment is made.
Advantages:
1. It is simple to operate and easy to understand. Since it is very easy the same is used in many advanced countries, viz. U.K., U. S.A etc.
2. It shows how soon the cost of purchasing an asset will be recovered. In other words, it considers the liquidity aspect of working on the ground that a project with short-pay-off period is better than those with long pay-off period.
3. Short-term approach reduces the loss through obsolescence particularly when there is any rapid technological development.
4. It considers risks as well which may arise due to the following:
(i) Political instability;
(ii) Nature of the product; and
(iii) Introduction of a new product.
5. It acts as a yardstick in comparing the profitability of two projects
6. In some cases. Pay Back Period is closely related to ARR and as such, enjoys the benefit of ARR. This is particularly applicable where the projects have substantially longer lives than their pay back periods and annual savings on cash inflows are comparatively uniform.
Disadvantages:
1. It recognises only the recovery of purchase costs, not profits earned during the working life of the asset.
2. It gives much stress on converting capital into cash, which is not important in case of those assets which have longer working life.
3. It does not recognise the time value of money.
4. It does not take into consideration that profits from different projects may assume at an uneven rate.
5. It ignores the basic fact that actual profitability depends on the number of years it will continue to operate after the pay-back period Thus, Profitability = Net cash flow or Saving × (Expected life of the project – Pay Back Period).
Pay Back Profitability:
This is a modified version of Pay Back Period Method. It recognises the fact that the total cash flow remains after recovering the cost of investment. Therefore, project will be selected on the basis of profitability after pay-off period.
Profitability is calculated as under:
Profitability = Net cash flow or Savings Earning × (Expected life of the project – Pay Back Period)
However, the following illustration will make the above principle clear:
Illustration:
There are two alternative machines. You are asked to compute the profitability of the investment on the basis of pay back profitability.
Solution:
It is evident from the above statement that while calculating profitability, Machine Y is, no doubt, profitable investment. But if the pay-back period, is considered, Machine X appears to be more profitable since its pay-back period is shorter, i.e., 5 years in comparison with Machine Y which has a payback period of 7 years.
As, the machine Y contributes Rs. 3,000 more (Rs. 18,000 – Rs. 15,000) after recovering its capital cost hence, it is more profitable to invest in Machine Y than in Machine X.
Pay Back Reciprocal:
It has already been explained that pay-back period expresses the profitability in terms of years and it does not reveal any return as a measure of investment. And, this pay back reciprocal is utilised in order to rectify the said situation. It is useful where the cash flow/earning is relatively consistent and the life of the asset is at least double the pay-back period. It may also be expressed as a percentage.
If the pay-back period is same as the life of the asset, the reciprocal would be one. As such, it is useful for long-term projects and it is also used as a guide to ascertain the discount factor in discounted cash flow calculations.
The Pay Back Reciprocal is computed as under:
Acceptance Rule:
The pay-back period may also be used as an accept-or-reject criterion along with a method of ranking projects for an investment proposal. In other words, if pay-back period is less than the maximum pay-back period which is set up by the management, it would be accepted, on the contrary, it would be rejected.
Similarly, as a ranking method, the project which has a shortest pay-back period will be assigned the highest rank and lowest rank is assigned to the highest pay-back period. Naturally, the projects with shorter pay-back period will be selected between the two.
Discounted Pay Back Period:
This method actually recognises the time value of money by combining payback with Net Present Value (Discounted Cash Flow). Generally, the NPV are added in a cumulative manner from the beginning of the project till the same becomes a positive one.
And the turning point is known as the discounted pay-back period of a project which is defined as the time when the capital so invested has been coming back with the interest cost of funds related to it.
Illustration:
Calculate the pay-back period from the following particulars using:
(i) The traditional method, and
(ii) The discounted pay back method.

Solution:
(i) Pay-Back-Period (under traditional method) –
(ii) Discounted Pay Back Period –
Advantages:
The significant merit of this method is that it incorporates the usual requirement to make some return on an investment. Secondly, the method of calculation helps in the selection of project risk. For example, in case of foregoing illustration, if nationalisation or take over in any form is expected with 7.55 years, the project itself proves a high risky one of never becoming profitable.
Capital Budgeting: Investment Criteria #
3.
Discounted Cash Flow Techniques:
The earlier two methods, viz. ARR method and Pay Back Period method, discussed so far for the purpose of appraising the investment proposals, do not consider the basic facts, i.e., the timing of cash flows.
Because, the Accounting or Average Rate of Return method recognises cash proceeds to the original or average cost of investment whereas Pay Back Period method considers all cash flows received before the pay-back period equal but do not consider the cash flow after pay-back period.
Thus, both methods fail to recognise the basic fact that the sum of money received in future is less valuable than it is to-day, i.e., the time value of money.
There are three reasons for this. They are:
(a) Re-investment opportunities,
(b) Uncertainty and
(c) Inflation
In order to overcome the shortcomings of ARR and Pay Back Period, Discounted Cash Flow (DCF) methods are recognised since they actually provide a more objective basis. The distinguishing feature of the DCF is that it recognises the time value of money. Moreover, the commendable characteristic of these techniques is that they consider all benefits and costs occurred during the life of the project.
At first, the DCF technique, viz. Net Presented Value (NPV). This is followed by the Internal Rate of Return (IRR) method.
There are two variations of the NPV method, viz:
(a) The Profitability Index or Benefit- Cost Ratio and
(b) Terminal Value method, which are subsequently discussed.
Before discussing the NPV method, we are going to explain the two concepts, viz Compounding (Interest) and Discounting (Present Value). It is known to all that interest rate is nothing but a rate at which one will be compensated for exchanging value now than it is later. The original amount/price is known as ‘principal’.
Here, the word ‘compound’ refers to add interest to principal at periodic intervals for the purpose of establishing a new basis for subsequent interest computations.
In other words, under this method, the interest of the first year is computed on the amount of principal, but the interest of the next (2nd year) year will be computed on the principal plus the interest of the first year and so on. This process continues till the end of the final year.
The following illustration will make the principle clear:
Suppose, the principal is Rs. 100. Rata of interest (compound) is 10% for five years. The compound interest will be calculated as under. (Calculation to be made to the nearest rupee). Prove it.
Solution:
By using the following compound interest formula the same (i.e. Rs. 161) can be computed as under:
It should be remembered that when the period ‘n’ is small application of logarithms is not necessary. The same can be found out by simple arithmetical calculations. However, the same result can also be ascertained with the help of discounting. Discounting is just the opposite of compounding.
In this case, we are to compute the present value which is to be received at a future period From the above example, if we want to find out the present values at the beginning of the respective years 1, 2, 3, 4 and 5; Rs. 110, Rs 121, Rs. 133, Rs. 146 and Rs. 161 respectively at 10% p.a., the result will be Rs. 100 in each case with the help of the said formula:
Capital Budgeting: Investment Criteria #
4.
Net Present Value Method (NPV):
The Net Present Value Method (NPV) is the time value of money approach to evaluate the return from an investment proposal. Under this method, we discount a project using the required return as the discount factor In other words, a stipulated compound interest rate is given and by the use of this percentage net cash flows are discounted to present values.
The present value of the cost of the project is subtracted from the sum of present values of various cash inflows. The surplus is the net present value. If the NPV is positive, the proposal’s forecast return exceeds the required return, hence, the proposals are acceptable.
But if the NPV is negative, the forecast return is less than the required return, the proposals is not acceptable. Thus, the decision rule for a project under NPV is to accept the project if the NPV is positive.
and reject if it is negative. Or,
(1) NPV > zero = Accept.
(2) NPV < zero = Reject.
Conversion of Net Cash Flow (NCF) into Present Value (PV):
a. By the use of Logarithms:
In case of uneven Net Cash Flows (NCF), the present value of a future sum may be computed with the help of the following formula:
V = A/(1 + i)n
Where,
V = Present Value
A = Annual Net Cash Flow (after tax but before depreciation)
i = Rate of Interest
n = Number of years,
where there are a number of years annual net cash flows, the above formula may be to:
However, if there is uneven net cash flows, the PV of various NCF must be computed separately which will result in tedious calculation. But, if there is an even rate, the following annuity formula may be used:
Therefore, any of the above three forms may be accepted. The following illustration will make the principle clear:
Illustration:
The management of a firm desires to purchase a machine. Two machines are available in the market — Machine A and Machine B You is asked to advise the management which of the two alternatives will be more profitable under the NPV method from the following particulars:
Solution:
Before taking decisions it is necessary to find out the present value of net cash flows from the alternative investments with the help of the following annuity formula:
It is evident from the above that Machine B will be the more profitable investment since the NPV of earnings in Machine B is greater than that of Machine A
b. By the use of Discount Tables:
Sometimes net cash flows (NCF) can be converted into NPV with the help of the discount table which reveals the present value of Re. 1 receivable at different intervals of time together with wide range of interest rates.
It should be noted in this respect that when there is expected uneven cash flows, each year’s NCF will have to be discounted separately in order to find out the NPV. But if there is even NCF, a general Present Value table is sufficient for the purpose.
Illustration:
Calculate the NPV for project ‘A’ which initially cost Rs 3,000 and generates annual cash inflow of Rs. 1,000, Rs. 900, Rs. 800, Rs. 700 and Rs. 600 in five years. The discount rate is assumed to be @10%.
Solution:
Net Present Value of Project A
Thus, it is possible to calculate the NPV for any series of future cash flows with help of the above procedure.It is needless to mention that if NCF accrues at even rate, the procedure is quite simple. For example, the future cash flow id Rs. 400 in a series which is to be received at the end of the next three years.
The above procedure may be neglected but the dame is computed as under:
This discount factor, i.e., 2,486 can be applied directly. Therefore, the P.V of Rs. 400 to be received annually for 3 years would be –
Rs. 400 x 2.486 = Rs. 994 (approx.).
Evaluation of NPV method:
Advantages of the NPV method are:
(i) It recognises time value of money.
(ii) It also recognises all cash flows throughout the life of the project.
(iii) It helps to satisfy the objectives for maximising firm’s values.
Disadvantages:
The NPV method has the following drawbacks:
(i) It is really difficult.
(ii) It does not present a satisfactory answer when there is different amounts of investments for the purpose of comparison.
(iii) It does not also present a correct picture in case of alternative projects or
where there is unequal lives of the project with limited funds.
(iv) The NPV method of calculation is based on discount state which again depends on the firm’s cost of capital. The latter is to some extent difficult to understand as well as difficult to measure in actual practice.
Capital Budgeting: Investment Criteria #
5.
Internal Rate of Return or Yield Method:
The Internal Rate of Return (IRR) method is the second discounted cash flow or time adjusted method for appraising capital investment decisions. It was first introduced by Joel Dean. It is also known as yield on investment, marginal efficiency of capital, rate of return over cost, time-adjusted rate of return and so on.
Internal rate of return is a rate which actually equates the present value of cash inflows with the present value of cash outflows.
It is actually the rate of return which is earned by a project, i.e. it is a rate at which the NPV of investment is zero. This method also recognises the time value of money like NPV method by discounting the cash streams.
Since it exclusively depends on the initial outlay and cash proceeds of the projects, and not by any rate determined outside the investment, it is appropriately called as Internal Rate of Return Under this method, the IRR should be compared with a required rate of return which is as the cut-off or hurdle rate.
A project is profitable only when the IRR is not less than the required rate, i.e. undertake any project whose internal rate of return exceeds required rate. In the opposite case, it is rejected.
In other words, where there are a number of alternative proposals, the acceptances criterion can be considered after analysing the following:
(i) IRR is to be found out in each alternatives cases;
(ii) Compare the IRR with cut-off rate and those projects are rejected whose IRR is less than the cut-off rate.
(iii) Compare the IRR of each alternative and select that one which produces the highest rate and most profitable one.
IRR can be found out by solving the following equation (mathematically), it is represent by the rate, r, such that:
where, C = Initial cash outlay;
P1, P2, P3, = Stream of future net cash flows.
The main shortcoming of this method is to ascertain the IRR which equates P. V. of NCF with that of initial cash outlay. In most cases, the rate is chosen at the first attempt and consequently one has to resort to trial and error (that is why this method is sometimes called ‘Trial and Error’ method).
Here, C, P, and n are all known and as such r can be found out by solving the
equations. But the difficulties arises since the value of log (1 + r)-n cannot be determined.
Naturally, after applying three or four trials runs, an area can be noticed, where the actual rate lies and simple interpolation or graph may be used in order to approximate the actual rate.
The above principles may be explained with the help of the following illustration under two conditions:
(a) Where there is even series of net cash flows:
Under the circumstances, initial cash outlay should be divided by the NCF per annum and locate the nearest discount factors. And choose that discount rate which corresponds to the approximate rate of return. For this purpose, simple interpolation may be used for accuracy. The following illustration will, however, make the principle clear.
Illustration:
Initial Outlay Rs. 40,000.
Annual Net Cash Flow (NCF) Rs. 12.,000
Estimated life 5 years.
Calculate the Internal Rate of Return (r) of the projects.
Solution:
In order to find out IRR, we are to calculate the rate which will actually equate the original investment (Rs. 40,000) with the present value of Rs. 12,000 received annually for five years.
Suppose, we start with 14% rate of interest. The present value of Re. 1 received annually for 5 years at 14% is 3.4331 which is the discount factor. At the same time, the total present value of Rs. 12,000 received annually for 5 years becomes Rs. 60,000 (Rs. 12,000 x 5) which actually comes to Rs. 41,197.2.
The present value of future cash streams exceeds the initial investment (i.e., Rs. 40,000). Alternatively it can be stated that the NPV> zero. As such, this rate is naturally not the IRR. As the NPV> zero we are to search for a higher rate of interest in order to have a lower NPV.
Let us try again on the assumption that the discount rate is 16%. Thus, the discount factor is 3.2743 which is multiplied by Rs 12,000 presents a total present value of Rs. 39,291.6. As a result, the present value of cash streams falls short of the outlay (by Rs. 708 4) and as such, the NPV < zero.
Therefore, the IRR lies between 14% and 16%. If we consider again 15% rate of interest which is 3.3522. In that case, the present value of Rs. 12,000 after five years will be Rs. 40,226.4, i.e. slightly more than the original outlay.
So, the IRR will be slightly more than 15% but not more than 16%.
However, the exact figure can be received by the application of the following interpolation formula:
Therefore, the IRR is 15.24%.
From the above, it is evident that the said principle is particularly applicable if there is a constant annual cash flow. But in actual practice, that is not always possible. The calculation in such a case is more difficult. This principle is explained below.
(b) Where there is uneven series of net cash flows:
It has already been stated above that if there is any uneven series of net cash flows, calculation is comparatively difficult In this case, in order to reduce the number of trial runs the first trial rate should be carefully selected It should be remembered that if net cash flow is not too uneven, selection of first rate may be considered as under:
When the first trial rate is applied for converting net cash flows to present values, the next trial rates can be selected on the basis of the following:
(i) When the present value of NCF is < the cost of the project = the second trial rate will be less than the first trial rate;
(ii) When the present value of NCF is > the cost of the projects = the second trial rate will be more than the first one.
In this manner, there will be a place where the exact discount rate will lie and the same can be ascertained with the help of simple interpolation.
The following illustration will help to make the principle clear:
Illustration:
A Co. Ltd. desires to purchase a new machine in order to increase its present level of production. Two alternative machines, viz., Machine X and Machine Y, are available in the market.
The details of the machines are given below:
You are asked to ascertain the more profitable machine (assume that the minimum rate of return laid down by the management is 16 % p.a.).
Solution:
The first rate is selected on the basis of the following Guide Rate:
Project X
Therefore, from the above statement it becomes quite clear that actual rate will lie between 15% and 20% which may be found out with the help of the following interpolation:
(Following the earlier method but by a different approach)
Project Y
The first trial rate is calculated as under:
Thus, the actual rate will lie between 10% and 15% which is calculated as under:
Comments:
Project X is to be undertaken by the management since it satisfies the norms prescribed by the latter (i.e., 16%) and also the rate of return is higher than the project Y.
Acceptance Rule:
It has already been highlighted in the present context that a project is profitable only when the IRR is not less than the required rate (which is known also as the firm’s cost of capital or cut-off or hurdle rate), i.e., when IRR is higher than or at least equal to the minimum required rate.
Similarly, in the opposite case, that is, if the IRR is less than the cost of capital, the project shall be rejected. For example, if the required rate of return was 12% and this criterion is used, the investment proposal considered above would be accepted.
If the required rate of return is the return, investors expect the firm to earn on the project, accepting a project with an internal rate of return in excess of the required rate of return should result in an increase in the market price of the stock, because the firm accepts a project with a return greater than that required to maintain the present market price per share.
Evaluation of IRR:
The Internal Rate of Return Method has the following advantages:
(a) It recognises the time value of money like Net Present Value Method;
(b) It also takes into account the cash flows throughout the life of the project;
(c) This method also reveals the maximum rate of return and presents a fairly good idea about the profitability of the project even if the firm’s cost of capital is absent since the latter is not a precondition for use of it;
(d) The percentage which is calculated under the method is more meaningful and justified and that is why it is acceptable to the users since it satisfies them in relation to cost of capital.
Although the IRR method is theoretically sound it is not even free from snags.
Some of them are noted below:
(a) The method of calculation is no doubt complicated and it is difficult to use and understand the same.
(b) This method does not present unique answers under all circumstances and situations. It may even present a negative rate or multiple rates under certain circumstances.
(c) This method recognises the fact that intermediate cash inflows which are generated by the project are re-invested at the internal rate whereas the NPV method recognises that cash inflows are reinvested at the firm’s cost of capital which is more appropriate and justified in comparison with IRR method.
(d) It may present inconsistent result with the NPV method when the projects actually differ from their expected life or cash outlays or timing of cash flows.
Net Present Value vs. Internal Rate of Return:
The Net Present Value and the Internal Rate of Return methods are closely related and time-adjusted investment criteria for measuring investment proposals. They do not, however, lead to the same decision. Because, under the NPV method, cash flows are converted into their present value with the help of a discount rate which represents the firm’s cost of capital and as such those proposals which result in negative NPV are rejected.
But, under the IRR method, also highlighted above, it has to be selected in such a manner that the present value of capital outlay must be equal to the present value of net cash flow (NCF). Here, there is no discount rate like NPV method. This method expresses the fact that the best investment will be one which will produce the highest rate of return at the time of equating the PV of capital outlay and PV of NCF.
The NPV and IRR methods are to some extent similar in certain respects. For example, they would present the same accept-reject decisions in some circumstances. But they differ in the sense that the results about the selection of an asset are mutually contradictory under certain conditions.
As such, a comparison is needed between the two methods when:
(i) There are similarities (between NPV and IRR methods) and
(ii) There are differences (between NPV and IRR methods).
These are discussed below:
(i) NPV and IRR: Similarities (i.e., in case of Independent Projects)
It has been explained above that NPV and IRR methods actually lead to the same acceptance or rejection decision rule where there is a single project.
That is due to:
(a) The discount rate which is greater than the IRR and as such, the NPV becomes negative;
(b) The required rate which is greater than the IRR and as such, the project is rejected.
Therefore, the situation where the two methods will present a concurrent accept- reject incisions will be in respect of conventional and non-conventional investment projects.
Conventional Investment:
A conventional investment is one whose cash flows take the pattern of an initial cash outlay followed by cash inflows. It has only one change in sign, e.g., – + + +……….
Non-conventional Investment:
A non-conventional investment is one of the cash outflows are not restricted to the initial period but are interspersed with cash inflows throughout the life of the project. It has more than one change in sign e.g., – + + + -………….
The NPV and IRR methods will result in the same accept-reject decisions rules where conventional investments are economically independent and where there are no constraints in accepting all profitable projects and same projects become profitable by both of them, viz., NPV and IRR.
The reason is very simple. Because, it may be recalled that, under NPV, a project will be accepted only when it has positive NPV, i.e. NPV exceeds zero (NPV >0) whereas under IRR, a project may be accepted when IRR is higher than the required rate of return (i.e., r>k) i.e., cost of capital.
If there is only one project there is actually no scope of conflict between NPV and IRR since they are used simultaneously for the purpose of measuring the investment. The principle followed by a diagram will help to make it clear.
By taking the figures of Project X from the previous illustration No. 14, a graph is plotted. The Net Present Value (NPV) of the project would be maximum, i.e. Rs. 62,500 (i.e., difference between total NCF – Initial outlay (Rs. 1,62,500 – Rs. 1,00,000) if the discount rate is assumed to be zero, although it is an unreal situation. When the discount rate increases, NPV starts decreasing. That is, at 19.35% the NPV is found to be zero.
IRR is calculated in this case which is also 19.35%. It is to be noted that two points, one representing the highest NPV and the other by IRR are joined. It is interesting to note that if the cost of capital is assumed to be 16%, the project may be accepted under the IRR method since IRR is greater than k, i.e., IRR>k- or, 19.35%>16%.
At 16% cost of capital, i.e. discount rate NPV is positive (which is represented by NPV value in the graph). Therefore, under NPV method the project may also be accepted.
On the other hand, when cost of capital is taken as 25%, the project is rejected since IRR<k i.e., 19.35%<25%. The NPV is also found to be negative at 25% which is represented by NPVo in the graph. Therefore, the same is also rejected.
Thus, Fig. 7.1 portrays NPV as (i) positive, (ii) zero and (iii) negative corresponding to three situations, viz., (i) IRR > k, (ii) IRR = k and (iii) IRR < k.
Thus, it can be stated that the two approaches lead to identical result about the accept-reject decision.
(ii) NPV and IRR: Differences (i.e., in case of Ranking Dependent Projects):
From the foregoing discussion we have seen that the NPV and IRR methods present the concurrent result in case of independent conventional investments. Sometimes they present contradictory result particularly when there are alternatives ways for achieving an objective — i.e., in case of mutually exclusive investment project.
Mutually exclusive means acceptance of one investment completely eliminates the expected proceeds of the other investment, or, in short, acceptance of an investment precludes the acceptance of others.
Now, this mutual exclusiveness of the investment project may be divided into two following groups:
(i) Technical:
It relates to the alternatives which have different profit-abilities and the most profitable one should be selected e.g., whether a firm should engage outside distributors or it should establish its own sales organisation for increasing sales.
(ii) Financial:
In case of resource constraints, a firm may be forced to accept only one project which is most profitable rather than accepting all the projects which exceed a minimum acceptable level. That is, if funds are limited and as a result of limited funds only one project is accepted, it is known as capital rationing.
Here, both the NPV and IRR methods may present conflicting rankings to mutually exclusive projects. It must be remembered that in case of dependent projects or mutually exclusive projects ranking of projects becomes actually critical and as such, we are to tackle the problem presented by NPV and IRR methods.
According to the authors, Weston and Brigham, conflicting ranking occurs under the following situations:
(i) The projects have different expected lives;
(ii) The cash outlay of one project is larger than that of the other;
(iii) The cash flow pattern of the projects may differ.
Project lives:
Where the lives of the projects are unequal, the NPV and IRR methods present a conflicting ranking to mutually exclusive projects.
The following example will help to make the principle clear:
Thus, from the above, it is found that the ranking given by two methods, viz. NPV and IRR is different. In other words, IRR method suggests Project X while, NPV method recommends Project Y.
Cash Outlay:
Another situation where the IRR and NPV methods present contradictory ranking, is when there is different size of initial cash outlay, i.e., if cash outlay of some projects is larger than that of others.
Consider the following example which will make the principle clear:
Thus, the two projects are ranked in a different manner. In short, NPV method recommends the Project Y whereas IRR method will suggest the Project X.
Cash Flow Timings:
The next contradictory ranking presented by NPV and IRR methods is the cash flow timings although the initial outlay of the projects may be the same, i.e, the mutually exclusive proposals may differ simply on the basis of cash flows generated. No doubt, it is a conflict in ranking of proposals presented by the NPV and IRR methods since they have different patterns of cash flows.
That is, in other words, if there are two or more investment proposals which are mutually exclusive they may present contradictory results and hence, ranking would vary according to the method followed. The following example will, however, help to understand the principle.
Note:
(Calculations of IRR and NPV are not shown) From the above, it becomes quite clear that if IRR is used, the decision will go in favour of Proposal I since it has the higher returns. On the other hand, if NPV is used as decisions criterion, it will go in favour of Proposal II since it has the higher NPV. Naturally, if one of them is to be selected, there will be a clear conflict between the two.
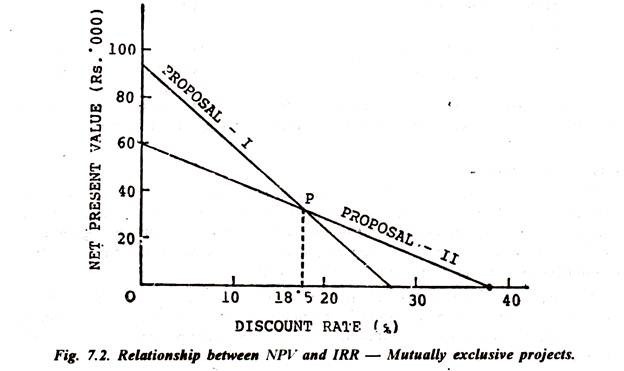
In order to suggest a remedy for resolving the conflict and also to explain the nature of the problems, the above illustration can also be graphically presented as under:
Fig. 7.2 portrays that when discount rate is assumed to be zero, the NPV will be Rs. 95,000 (Rs. 1,65,000 – Rs. 70,000) and Rs. 60,000 (Rs. 1,30,000 – Rs. 70,000) respectively for proposals 1 and II, the IRRs are 23.33% and 37.62% respectively. Needless to mention that in the above diagram, IRR is plotted on X-axis whereas NPV is plotted on Y-axis.
It is seen from the above that when the discounting rates are increased, NPV starts to decline and as such, NPV is zero corresponding to 27.33% (IRR) in case of Proposal I whereas in case of Proposal II it is 37.62%.
Similarly, Proposal II (at zero discount rate) shows highest NPV in Y-axis corresponding to an IRR of 27.33% in X-axis. These two points are joint to form a straight line. Same procedure is also to be adopted in case of Proposal II. Then, the two lines intersect at a certain point, viz. P.
Hence, this discounting rate corresponding to intersection point is about 18.5%. Naturally, if there is any discounting rate which is below 18.5% the two methods would rank them in a different manner.
For example, the NPV of Proposal I is higher in comparison with Proposal II (if discounting rate is 10%) and hence, it is preferable to use NPV method. On the contrary, IRR of Proposal I is 27.33 as against 37.62 of Proposal II. That is, there is a clear conflict. But, if discounting rate exceeds 18.5% there will be no conflict between them.
The general principal about the conflict between NPV and IRR is that if the IRR is greater than the rate at which the NPV of mutually exclusive projects are equal, both of them will present the compatible result, i.e. if there is a higher IRR in any project, there will also be a higher NPV.
On the other hand, if the IRR is less than the rate at which the NPV of mutually excessive projects are equal, both of them will present a contradictory result. In other words, the projects with lower IRR will have higher NPV or higher IRR with lower NPV.
Re-investment Rate Assumption:
The foregoing discussions have already highlighted that the NPV and IRR methods would rank projects in a different manner in case of mutually excessive projects provided that there is (i) initially a different cash outlay, (ii) different pattern of cash flows, and (iii) unequal service life of the projects, although ranking given by NPV is theoretically more sound.
Practically, the conflicts between the two methods are primarily due to the different assumptions about the re-investment rates.
IRR method is deficient since it attempts to find an interest rate which will equate the present value of a projects’ proceeds with that of its investment outlays, i.e. to find an average yearly rate of return which just equates the two.
Therefore, using the IRR method for ranking is equivalent assuming that any intermediate cash flows from a project will be re-invested to earn the projects’ internal rate of return, while the NPV method hypothesizes that such cash flow streams will earn only interest equal in value to the discount rate.
The re-investment assumptions of the NPV method, on the other hand, seem to make economic sense where everyone can borrow or lend at the going rate of interest. Under the circumstances, any project which offers a return higher than the market rate of interest will always be accepted.
Thus, the existence of intermediate cash flows does not make possible the acceptance of any additional project yielding more than the market rate of interest.
This re-investment assumption is merely a specific application of the NPV model’s general assumption that the discount rate reflects the opportunity cost of capital. As such, discounting at the going rate of interest recognises that with a perfect capital market the sacrifices of accepting any specific project is measured either by the cost of borrowed funds or by the interest foregone if internal funds are used.
Again, extra emphasis is imposed on IRR since under this method, different cash flow streams for each investment proposals will constitute the different investment rates. As such, there will be as many rates of re-investments as there are investment proposals which are to be measured. This re-investment rate and IRR method can be demonstrated with the help of the following hypothetical examples.
According to IRR method, here both the projects, A and B, have a rate of return @ 100% (i.e., if Rs. 100 are invested for one year @ 100%, it will amount to Rs. 200, similarly, if investment for two years, it will grow Rs. 400). As both the projects present the same IRR, the firm may accept any one of them or, it should be indifferent about their acceptability.
In order to be true it must be necessary that Rs. 200 which is received at the end of first year must be Rs. 400 at the end of second year, i.e., the rate of earning must have to be the same i.e. at 100%. If the rate of earning is not the same, i.e. 100%, Rs. 200 will not be Rs. 400 at the end of second year.
And, in that case, if Rs. 200 is not transformed to Rs. 400 at the end of second year we cannot give the equal rank of the two projects. Of course, the fact that a firm may find other investment opportunities at the required rate is ignored.
However, the present value method is free from the said snag. The principle is explained here by taking the same example to be prepared under NPV method assuming that the cost of capital (k) is @ 10%:
From the above it becomes crystal clear that according to NPV method, project B is more profitable than project A since the later has a higher NPV in comparison with the former. It is needless to mention that the re-investment rate, here, is more realistic, reasonable and dependable.
The re-investment rate assumption about the cash flow generation is, theoretically more correct and appropriate under NPV method than the IRR method since the rate itself is consistent in case of NPV itself while in case of IRR it is widely varied. Moreover, the IRR method also suffers from computational problem, i.e. it is difficult to calculate.
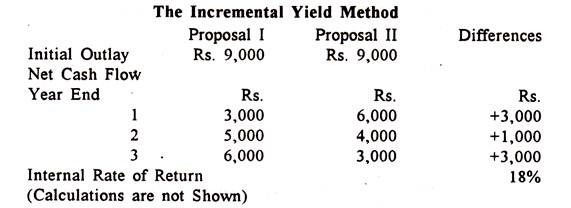
The Incremental Method:
It should be remembered that the correct comparison between Proposal I and Proposal II must not be in terms of average yearly yields but the same should be in terms of cash flow differences between the two projects.
In other words, using Proposal II as base, the incremental investment in order to obtain Proposal I should be compared with the consequent incremental cash flows. The question is after having accepted Proposal II, may we realise a better return from Proposal I?
Consider the following table for the purpose:
Thus, the switch to Proposal I entails foregoing Rs. 3,000 in year I as against extra cash flows of Rs. 1,000 and Rs. 3,000 in years 2 and 3 respectively. The IRR in this case is 18% which is greater than the cost of capital.
Therefore, Proposal I is better than Proposal II and hence it should be accepted despite the fact that its IRR is 22.5% in comparison with Proposal II which has an IRR of 24%. Thus, the modified method of IRR will actually lead to same conclusion as arrived at under NPV method.
Problems of Multiple/Dual Rates:
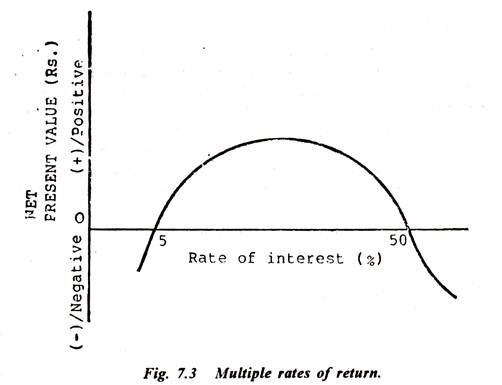
Another serious difficulty associated with IRR method is that it can yield multiple internal rates of return, i.e. the projects which have non-conventional cash flow patterns may have multiple rates of return. For example, the cash flow series, — Rs. 1,000 + Rs. 2,550, — Rs. 1,575 has IRR of 5% and 50%.
This is shown in figure 7.3 where NPV curve intersects the horizontal axis twice:
It should be remembered that multiple rates arise since several different interest rates may equate the present value of cash inflow of a project to the present value of its initial outlay.
This happens simply because different interest rates may present different values to each and every component of a project’s cash flows, i.e. very high rate of interest will give a low value to all but a project’s near cash flows, and on the contrary, very low rate of interest presents all cash flows almost nearly equal value.
As such, since the interest rate tends to zero, the P.V. of a project will approach the algebraic sum of its undiscounted cash flows and will be negative if this is negative. In the diagram, it is shown that at all interest rates below 5%, the negative third term of the project exceeds the weight of its positive middle term and produces a negative (-) PV.
And with a cost of capital higher than 5%, the positive second term in the cash flow pattern will be less sensitive to change in discount rate than the third term.
The P.V. of cash inflows, with these rates of interest, will exceed the weight of the two negative cash flows and give the project a positive (+) NPV. Similarly, if the rate of discount rises continuously, the negative (-) third term of the project will not be significant but the positive (+) cash flows will fall in value comparatively fast than the negative (-) first term.
Therefore, the value of the negative (-) terms will exactly offset, at some specific rate of interest, that of the positive (+) second term and as a result, the NPV curve will intersect the horizontal axis again. G. D.
Quirin has rightly said in his book, (‘The Capital Expenditure Decision’) that when multiple rates of return exist there seems to be no mathematical or economic grounds for specifying any one of them having value of more than — 100% as the IRR for all are the roots of a single polynomial equation.
Capital Budgeting: Investment Criteria #
6.
Profitability Index (PI) or Benefit Cost Ratio (B/C Ratio):
Another time-adjusted techniques for evaluating investment proposals is the Profitability Index (PI) or Benefit Cost Ratio (B/C Ratio). It is the relation between present value of future net cash flows and the initial cash outlay, i.e. this ratio is computed by dividing the present value of net cash flows by the initial cash outlay.
It is computed as under:
It is similar to the NPV approach. It measures the present value of return per rupee invested. Whereas NPV depends 011 the difference between PV of NCF and PV of cash outflow. This is actually a drawback of NPV method which has been mentioned above since it is an absolute measure, PI, on the other hand, is a relative measure.
Illustration:
Calculate the NPV and PI of the project assuming that the discount factor is 10%.
Solution:
Under this method, it should be remembered that an investment proposal may be accepted when the Profitability Index (PI) is greater than one. However, in case of mutually exclusive proposals, the acceptance criterion will be: the higher the index, the more profitable is the proposals and vice-versa.
Example:
(Data are taken from the previous illustration):
Thus, Investment in Machine B will be more profitable. It may also be done with the help of ranking. That is, highest rank will be given to that project which has highest PI.
Acceptance Rule (i.e., Accept-Reject Decision):
That an investment proposal is accepted when the PI is greater than one. When PI equals to I, the firm is indifferent to the project. Similarly, where PI is greater than, less than or equal to 1, the NPV is greater than, less than or equal to O respectively, i.e.
ADV.FM. 19
NPV will be positive = PI>1
NPV will be negative = PI<1
Therefore, NPV and PI present the same result about the investment proposals.
Evaluation of Profitability Index:
Like other DCF techniques, PI is, no doubt, conceptually sound since it satisfies almost all the requirements of appraising investment project, viz. time value of money, totality of benefit etc. Although it involves more calculations than the traditional methods (viz., ARR or Pay-Back Period Methods) but it is less than the IRR method.
According to this method, it has already been stated, ranks are assigned to the projects on the basis of PI and naturally, higher ranks will be given to the project which has highest PI.
Capital Budgeting: Investment Criteria #
7.
Terminal Value (TV) Method:
Under this method, it is assumed that each cash inflow is re-invested in another asset at a certain rate of return and calculating the terminal value of net cash flows at the end of project life. In short, the NCF and the outlay are compounded forward rather than backward by discounting which is used by NPV method.
The following illustration will make the principle clear:
Illustration:
Solution:
Before preparing the table we arc to know that we will re-invest Rs 8,000 (which is received) at the end of year 1 for 4 years 6%. The NCF of year 2 will also be reinvested for 3 years. Similarly, the NCF of year 3 will be re-invested for 2 years and so on.
Naturally, there will be no re-investment at the end of 5th year Therefore, the total sum of these compound NCF is then discounted back to the present at (k) in order to compare the PV of cash outflow which in this case is Rs 20,000
PV of Terminal Sum is shown below under consideration that the cost of capital is 10%.
Here the discount rate represents the cost of capital (k) (10%). We are also to find out the PV of Rs. 45,592 which will actually be received at the end of five years.
Therefore, the PV of the total compounded sum will be calculated as under:
PV = Rs. 45,592/(1 + .10)5 = Rs. 28,313
(Note: PV of Re. 1, received 5 years @ 10% discount rates is 0.621. The sum of the PV will be Rs 45,592 x 0.621 = Rs 28,313.).
Since TV is positive here, the project can be accepted. Its TV is Rs. 8,313.
Acceptance Rule:
From the foregoing discussion it becomes clear that if the value of the total compounded re-invested cash flows is greater than the present value of outflow, i.e. if NCF have a higher terminal value in comparison with the outlay, the project is accepted and vice-versa.
The accept-reject rule can, thus, be formulated as under:
(1) If there is a single project:
Accept the project if the terminal value (TV) is positive.
(2) If there are mutually exclusive projects:
The project will be more profitable which has a highest positive terminal value (TV).
It can also be stated that if TV is positive, accept the project and if TV is negative, reject the project.
It should be remembered that TV method is similar to NPV method. The only difference is that in case of former, values are compounded while in case of latter, values are discounted, of course, both of them will present the same result provided the rate is same, (i.e., discounting and compounding).
Taxation Effect:
Net cash flows are calculated after tax but before charging depreciation. As such, it requires explanation about the relevant provisions for depreciation and other allowance/charges which are contained in the income-tax Act, 1961.
They are:
(1) Normal Depreciation [Section 32 (1) (i) and (ii)]:
Such depreciation is allowed at prescribed rates on actual or written down value (WDV) of building, machinery, plant or furniture u/s 32(1), (ii) and on actual cost of ship u/s 32 (1) (i). Where the actual cost of any machine or plant does not exceed Rs. 5,000, the actual cost thereof shall be allowed as a deduction.
No normal depreciation will be allowed on asset sold or discarded or has been destroyed after using a part of the year.
Normal depreciation will be allowed on an asset in full on the basis of Diminishing Balance Method at prescribed rates even if it worked only for the last day of the year But it should be remembered that whatever method is followed, the amount of depreciation is to be added back to the profit after tax in order to ascertain the net cash flow for a specific period.
(2) Initial Depreciation [Section 32(1 )(iv) and (v)]:
Initial depreciation is allowed on assets in the following two cases, viz., in respect of erection of a building or installation of an asset:
(a) At the rate of 40% of the actual cost of a building, which has been newly erected after 31st March, 1961;
(b) At the rate of 25% of the actual cost of a building erection of which is completed after 31st March, 1967.
This initial depreciation shall not be deducted in determining the written down value of an asset, but it should be taken into account in ascertaining terminal allowance u/s 32(l)(iii) or Balancing Charge u/s 41(2) on disposal or destruction of such building or asset.
Terminal Depreciation [Section 32(l)(iii)]:
According to Section 32(l)(iii) in the case of any building, machinery, plant or furniture which is sold, discarded, demolished or destroyed, the amount by which the money payable in respect of such asset together with the amount of scrap value, if any fall short of the written down value, thereof, as reduced by initial depreciation, if any, shall be deductible by way of terminal depreciation or allowance provided such deficiency is actually written off in the books of the assesses.
Terminal depreciation cannot be claimed if the asset is not used for the purpose of business or profession.
Balancing Charge [Section 41(2)]:
According to Section 41(2), where any depreciated asset, such as, building, machinery, plant or furniture, which are used for the purpose of business or profession is sold, discarded, demolished or destroyed and the money paid or payable in respect of such asset together with the scrap value, if any, exceeds the written down value, so much of the excess as does not exceed the difference between actual cost and the written down value, i.e., the total depreciation (including initial depreciation, if any) allowed up to date, shall be chargeable to income-tax by way of Balancing Charge, and the remaining surplus, if any, is taxable as capital gains.
It may be mentioned here that where the insurance company replaces the asset lost or discharge the liability in respect of claim for asset lost under conditions of the policy, question of Balancing Charge will not arise in that case as there is no payment of money. The rules laid down by explanation 2 to Section 32(l)(iii) in respect of terminal depreciation are applicable in case of Balancing Charge.
Practically, the amount of balancing charge will bring down the amount of net cash flow or the amount realized on sale by the amount tax is payable on such Balancing Charge. In order to encourage the development of industries, development rebate was also introduced by the Finance Act, 1955 (Section 33) in respect of certain machinery or plant apart from the provisions already discussed above.
Working Capital:
Requirement of additional working capital in the various components of additional current assets, viz. Inventory (raw materials, work-in-progress and finished goods), as well as to pay off wages and other bills, is needed in addition to the investment in fixed asset on a project. Therefore, while determining total amount of investment, requirement of additional working capital should also be taken into consideration.
Similarly, when the project comes to an end, the amount of working capital (in full or in part) so realized, should also be considered along with the scrap value of fixed assets, if any. Sometimes, a run-down of working capital investment may so happen before the project actually conies to an end. In that case, the release of funds must be considered in the respective years during the life of the project carefully.
The following illustration will, however, make the principle clear:
Illustration:
Initial depreciation is @ 20%.
Scrap value of the investment will fetch Rs. 3,122.
Cost of capital is @ 10% p.a.
Advice management as to the profitability of the assuming that the working capital can be recovered in full at the end of the project life.
Solution:
Working:
Thus, the total amount of discounted cash flow at Rs. 27,771 exceeds the total cost of investment (both fixed capital and working capital, i.e., Rs. 20,000 and Rs. 40,000) = Rs. 24,000. Hence, the project should be accepted. If, however, the Profitability Index (PI) is considered, the same is found to be 1.16 (i.e., Rs.27,771/Rs. 24,000).
Capital Rationing:
From the foregoing discussion it may be recalled that the profitability of a project can be measured by any one of the DCF techniques, (viz., IRR, NPV and PI) particularly the two theoretically sound methods IRR and NPV.
Practically, the firm may accept all those projects which give a rate of return higher than the cost of capital or, which have a positive NPV. And in case of mutually exclusive projects, the projects having the highest NPV or giving the highest rate of return may be accepted In other words, a firm should accept that investment proposal which increases by maximizing firm’s value.
In actual practice, however, every firm prepares its annual capital expenditure budget which depends on the availability of funds with the firms or other considerations. In that case, a firm has to select not only the profitable investment opportunities, but also it has to rank the projects from the highest to lowest priority, i.e., a cut-off point is selected.
Naturally, the proposals which are above the cut-off point, will be funded and which is below the cut-off point will be rejected. It should be remembered that this cut-off point is determined on the basis of the number of projects, funds available for financing capital expenditure and the objectives of the firm.
That is, in other words, question of capital rationing appears before us. It is normally applied to situations where the supply of funds to firm is limited in some way. It, actually, encompasses many different situations ranging from that where the borrowing and lending rates faced by the firms differ to that where the funds available for investment by the firm are strictly limited.
In short, it refers to a situation where the firm is constrained for external, or self-imposed, reasons to obtain necessary funds to invest in all profitable investment projects, i.e., a situation where a constraint is placed on the total size of capital investment during a particular period.
In the circumstances the firm has to select a combination of investment proposals which provides the highest NPV subject to the budget constraint.
Selection Process under Capital Rationing:
Needless to mention that under capital rationing a firm cannot accept all the projects even if all of them are profitable. In order to select or reject the projects, a comparison must be made among them.
Selection of project actually depends on the following two steps:
(i) Ranking the projects according to the Profitability Index (PI) or Net Present Value (NPV) method;
(ii) Selecting projects in descending order of profitability (until the funds are exhausted).
The projects can be ranked by any one of the DCF techniques, viz. IRR, NPV and PI. But PI method is found to be more suitable and reliable measure of profitability since it determines the relative profitability while NPV method is an absolute measure of profitability.
Illustration:
Funds available for capital expenditure in a year are estimated at Rs. 2,50,000 in a firm. The profitability index (PI) together with mutually exclusive investment proposals.
Which of the above projects should be accepted?
Solution:
The projects should be selected on the basis of profitability under PI method and rank is assigned accordingly, subject to maximum utilization of available funds.
These are shown below:
From the above, it becomes clear that the first projects should be selected as the optimum mix since they will completely utilise the available funds amounting to Rs. 2,50,000. Projects P6 and PB are not included in above as their PI is less than unity (1) and hence, these are to be rejected.
Illustration:
The following investment proposals along with their profitability index (PI) are presented below:
Solution:
Profitability statement on the basis of PI method is presented below:
Here, P1, ranks first. But it does not utilize fully the available funds. If P3 is selected alone, it will be worse than P1. Similarly, P1, and-P3 cannot be selected since their total requirements become Rs. 1,00,000 (Rs. 60,000 + Rs. 40,000) which is more than the available funds, viz., Rs. 75,000.
Therefore, if P3 and P4 are selected, available funds can completely be utilized. As such, the mix (P3 and P4) will be the most profitable projects and they will maximize the present value.
Thus, the total NPV of proposals 3 is highest in comparison with proposals 1 and 2. As such, the firm, in this case, will be able to utilize its scarce resources for optimum use.
Project Indivisibility:
It has been highlighted above that selection of project must be in such a manner so as to maximize profitability subject to the budget ceiling. Naturally, if this is strictly followed then it is better to accept many lower order smaller projects (according to ranking) than to accept a single large project. Therefore, under capital rationing, a possibility of trade-off arises between the two types of projects.
In other words, if a single large project is accepted, a series of small projects are rejected due to this indivisibility, i.e. a project is an entity to be accepted or rejected as a whole. It should be remembered that the problem of indivisibility may prove to be serious and make the entire selection process quite un-widely. The most efficient way for solving the same is the integer programming.
Ranking-Error Problem:
We know that any one of the DCF techniques can be used for ranking. Since there are different cash flow timings the three DCF techniques, viz. IRR, NPV and PI present conflict in ranking as to the project which is known as ‘Ranking-Error Problem”. The following illustration will make the principle of ‘Ranking-Error Problem’ clear.
Illustration:
From the information presented below, rank the projects after applying IRR, NPV and PI when each of them is as under:
Solution:
Ranking by IRR, NPV and PI is as under:
From the above, it becomes clear that the three DCF criteria rank the different projects in a different way. Needless to mention that if there is no limit of funds, all the projects (excluding P2) could be accepted by all the criteria. But, if capital is rationed, different decisions are reached by each criterion.
That is, the IRR would suggest to accept projects P3 P4 whereas the NPV would suggest to accept projects P1, P4 and the PI would suggest to accept projects P1, and P5 respectively. Naturally, the question arises before us which one is the ‘correct criterion’? This problem arises due to the differing timing of the cash flow. However, this problem can be tackled if a common re-investment rate is considered.’
Capital Rationing Using Graph:
Sometimes funds for investment are strictly limited in the current period. After that the same are freely available at the prevailing rate of interest. Of course, if there is any liquidity crisis in a firm, it will find out some financing sources even if the rate of interest becomes very high although the financing sources are limited.
The effect of limits on funds can be portrayed with the help of a diagram (Fig. 7.4) presented below, where amount of capital in a period is shown on the horizontal axis whereas (average) cost of capital is shown on the vertical axis.
The supply of capital at different costs of capital/prices is shown by AA curve. The increasing slope of the said curve (AA) reflects the higher marginal cost of each extra increment of funds. Curve BB represents the usual demand curve for funds. Here, projects are ranked inversely in order to diminish profitability.
As such, any point on this line shows the funds which are needed to finance those projects which have positive (+) NPV. (Where discounted at the cost of capital shown horizontally opposite on the y axis i.e. OD funds will be demanded when average cost of finance is OG).
Under the situation, the firm will try to utilize that amount of funds which are indicated by the intersection of the demand curve (BB) and supply curve (AA). In the present case, the firm must raise OD funds and finance those projects which are represented by the BH segment of BB.
It will give the greatest increment in net present worth. That is, each project to the left of H has a positive (+) NPV if discounted at OG and at this rate of interest the marginal project has a zero (0) NPV.
Therefore, from the above, it may be stated that the marginal project which is accepted simply covers its cost and all other projects which are accepted yield a return over and above their financing which are indicated by the area covered by the line GHB in the diagram.
If, on the other hand, investments cannot exceed, say, OC, the shareholders (equity) will forgo the NPV from those projects represented by EC. In that case, cost to equity shareholders is represented in the diagram by the area covered by EFH which reveals the excess returns over the average cost of capital.