Top 3 Models of Voting Theory

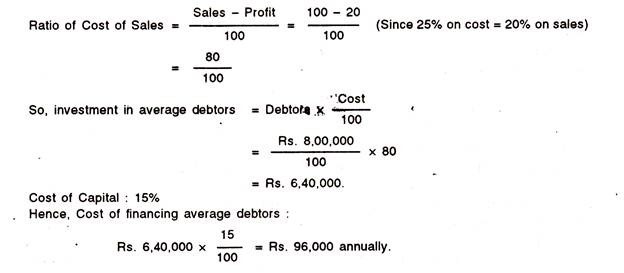
This article throws light upon the top three models of voting theory. The models are: 1. The Optimal Constitution 2. The Bowen-Black Majority 3. Log Rolling-The Buchanan Tullock.

Voting Theory: Model # 1. The Optimal Constitution:

Provision of public good presupposes the co-operation of the citi­zens. Without mutual co-operation through a representative gov­ernment or otherwise, the free rider problem will make ineffective the efficiency in Allocative mechanism.

By co-operating with each other people frame some sort of arrangements to exploit the gain associated with trade in public goods. Buchanan and Tullock conceived of a voting process for a public good as a method of exploiting the gains from such trade.

Buchanan and Tullock states that the analysis of any voting process to determine the level of public expenditures and individual taxes presupposes a voting rule to determine when a proposed measure passes. Larger the propor­tion of voters required to support the measure, the voting process will come closer towards exploiting all the gains from trade.

How­ever then the decision making process will be costlier is terms of time and costs involved is getting the requisite number to agree the proposal. Buchanan states that there is therefore a trade-off between exploiting the gains from trade and the cost of decision making in choosing an optimal constitution or voting rule.

Every voting rule involves two cost functions for the represen­tative individual. They are external cost function and decision making cost function.

The external cost implied in a voting rule is defined as the expected loss in utility in future voting decisions compared with the situations in which all the gains from trade are collectively exploited (a pareto optimum situation) is this sense external cost to an individual includes any expected reduction in utility due to departure from pareto optimality or due to adverse redistribution of income.

This external cost ‘C’ rises as ‘n’ (The proportion of the population that must vote for the proposal for it to pass) falls. The reason is that if fewer people are required to agree, the chance that an individual will be faced with a decision that doesn’t suit him rises.

Similarly the decision making cost function is defined as the cost that society incurs for taking a decision through the political process. As the proportion of people required to vote for a proposal in order for it to pass rises, these administrative and other cost also rise.

The decision making cost of a voting rule include the time and effort required to secure agreement for a proposal. As the proportion ‘n’ of votes required increases the decision making costs rise. Curve ‘D’ represent the decision making cost function. And curve ‘C’ also shows the external cost function for represen­tative individual.

Curve ‘C’ also shows the external costs for a representative citizen are expected to fall as the proportion of voters required for a decision rises.

According to Buchanan and Tullock the optimum constitution (i.e. the determination of opti­mum proportion required to vote for a proposal in order for it to pass) is one which minimizes the sum-C + D of these costs. A diagrammatic representation of the situation of optimal constitutions is given in graph 2.12.

In figure 2.12, the ‘C’ and ‘D’ costs are depicted as functions on ‘n’. Curve ‘C’ depict the external cost function. The curve C + D represent total cost. The optimum Constitution is one which minimizes C + D.

The representative individual in the figure will prefer that voting rule which minimizes the expected total costs (C + D) of the collective decision making process. That will be the voting rule given by n_O which Buchanan and Tullock call the optimum constitution.

However there are some conceptual problems associated with this optimum constitution. In order to define his external cost func­tion ‘C’ the representative individual (voter) must know his utility in Pareto optimum.

However it is a reality that there is infinite mul­tiplicity of Pareto optimum allocations, Therefore the definition of ‘C’ is ambiguous. Another serious problem with this method of choosing the optimum constitutions is that n_o may not be the same for everyone.

Then it is very difficult to establish a uniform rule for vote counting. In-spite of these problems Buchanan. Tullock mechanism provides an opening to the question of the best method of counting votes to economic analysis.

Voting Theory: Model # 2. The Bowen-Black Majority:

This method is the earliest model of public goods output determi­nation, through voting process. This model tries to show that if tax shares are given, the output of good which would be preferred by a majority would be uniquely determined and under certain conditions would even be optimal.

Suppose that a public good can be produced at constant marginal cost ‘MC’. Assume that the cost of the public good is to be equally divided among all members (N) of the society. In this case each individuals cost share is MC/N.

If MRS’ is the marginal benefit to individual i from the public good, the optimal output of public good is given when EMRS’/N = MC/N. In other words it means that the marginal benefit of the mean individual equals the per person cost of the public good.

Let us take an example to analyses the case of simple major­ity voting rule. Arun (A), Bhaskar (B) and Chetak (C) are three house owners residing nearly. They have to take a decision on a proposal regarding the width of a new bridge to be constructed.

Connecting their house property to a new road highway. Further assume that house owner Arun (A) possess a small car, Bhaskar. (B) A medium sized car and Chetak (C) A big and wide truck the cost of the bridge are to be equally born by the three house owners. In this situation, regarding the width of the proposed bridge, each make different option based upon his benefit.

Arun (A) favour a bridge with narrow width, Bhaskar (B) medium width and Chetak (C) A bridge with wide width. Under the rule of simple majority, in-spite of the different idea about the width of the bridge they have to arrive at a compromise for the common cause.

Any how a narrow bridge is having minimum acceptance. When the process of voting arise regarding increasing the width of bridge from narrow to medium, the vote is 2 to 1 in favour.

Considering the situation of increasing the width from medium to wide, the vote is 2 to 1 against. In this case medium width is the compromise solution. Therefore the median voter Bhaskar (B) is the one whose prefer­ences are agreed upon in the voting process.

The median voter is the one who lies between an equal number of voters who prefer one extreme (a narrow bridge) and an equal number who prefer the opposite extreme (a wide bridge).

In simple majority rule the medium voter’s majority rule in called medium voter theorems or model. Medium voter theorems are the proposition that preferences of the median voter are choose when several conditions such as all pref­erences being single peaked are present.

The Bowen- Black majority voting model can be explained with the following diagram. 2.13 (a). In the figure MC/N represent the constant marginal cost schedule pertaining to the production and supply of the public good. (I.e. the cost is equally shared among N numbers of the society).

The demand for the public good (MRSⁱ) is drawn through six schedules viz. a,b,c,d,e,f, and g, The mean individuals demand (εMRS /N) is also show in the figure. Thus X* is optimal supply of the public good. Persons with demand schedules e, f and g want more than x while the remaining person want less. Now suppose that the demand is normally distributed around X*. (as mean ).

Now suppose that X* were put to vote and a majority was needed to turn it down, X* will win. The reason why X* will win is that X* also happens to be the median demand. Therefore Black point out that if individuals have single peaked preferences the median would always win under majority voting rule.

Moreover the majority voting frame work does not always translate changes in preference of voters into changes in policies. Thus the analysis of Black generalized the circumstances under which majority rule would result in the preference of the median voter.

He showed that under majority rule, the preference of the median voter will be accepted by a majority over all other option or potential out comes when preferences of all voters are single peaked. The meanings of Single peaked preference are depicted in figure No. 2.13(b).

Preferences of five people over various outcomes, which are outputs of the public good, are shown in figure 2.13. (b). Each individuals preferences peak out at only one output of the public good. That is for individual 1 Q₁ is the most preferred output, for individual 5, Q₅ is the most preferred output.

Such preferences are single peaked. Four individuals would want more than Q₁ unit of the public good. Similarly four people would want less than Q₅ unit of the public good. The only output level which would win under majority voting is Q₃.

In Bowen’s analysis each of the voters has single peaked preferences when the output of the public good is measured along the horizontal axis. Black’s proposition is that whenever all preferences are single peaked, majority voting will select the output most preferred by the median voter over all other outcomes.

The absence of single peaked preferences may give rise to a well-known problem in voting theory. This problem is known as cyclical majorities or the intransitivity of the social preferences under majority voting. Consider a society consisting of three indi­viduals with three choices put to vote.

Social decisions are ex­ecuted through majority voting rule. The preferences of the three individuals over the three outcomes are explained with the help of the table and diagrams 2.14.

Assume that voters ‘A’, ‘B’ and ‘C’ have to choose among three alternatives ‘X’, ‘Y’ and Z by majority rule. Preference ordering of A, B and C is given in the table, and graph. The preference ordering is not single peaked for all individuals, and there is no way of ordering X, Y and Z, along the horizontal axis, so as to obtain them.

Let us examine the effect of majority voting among the various pairs of outcome. In a vote between ‘X’ and Y projects ‘X’ would win by two votes (A, C) to one (B). Likewise between ‘X’ and ‘Y’, ‘Z’ would win by two votes (B, C) to one (A). In this situation no one outcome can command majority support over all other and the outcomes is uncertain.

Here the social preference established through majority rule are said to be intransitive. The definition of transitivity of preferences is that if ‘X’ is preferred to ‘Y’ and ‘Y’ to ‘Z’ then ‘X’ will be preferred to ‘Z’. This property which is a condition of rationality for individual voters is satisfied for the collective decision process.

Voting Theory: Model # 3. Log Rolling-The Buchanan Tullock:

Buchanan and Tullock explore two important aspects of the political decision process in majority voting rule.

Firstly irrespective of how much anyone pays for the public good he has only one vote which is exactly alike every other vote.

Secondly issues are not decided independently. Thus if an individual doesn’t particularly care for an issue he might be persuaded to vote for it by some other individual in exchange for a promise that the later individual will support, at some time in the future, a proposal that the former individual does care for.

Thus vote trading or log rolling is a feasible option. One of the main contributions of Buchanan and Tullock is to consider the positive effects and optimality properties of the process of logrolling which is assumed to exist in political process.

Logrolling is a process of trading votes to achieve the majority necessary for approval. It is the trading of votes in situation includ­ing multiple issues where voters are trying to further their wellbeing. The phenomenon of logrolling can be explained with an example.

Suppose that we have three voters: A, B and C. Three spend­ing proposals are being considered: Construction of a stadium, construction of a hospital and construction of a school. ‘A’ is the only voter who favors the project stadium (the other two oppose it), ‘B’ is the only voter who favours proposal for hospital and ‘C’ is the only voter who favours an school programme.

The following table, for example shows the hypothetical benefit that voter A, B and C receive from the proposals if there are collective agreements to build a stadium a hospital and a school. Benefits tend to differ between individuals.

The net benefit as shown in the table equal to benefits minus costs, and hence total net social benefits equal the sum of net benefits that each individual receive from each project.

The perusal of data given in the table clearly shows that each individual has a strong interest in having one project funded. A having a strong interest is stadium, B for Hospital and C having strong preference for school.

Since one individual supports any one project, no project is under taken under a rule of simple majority. This however may not be the outcome. The logrolling between ‘A’ and B can result in a net gain to both parties.

By agreeing to vote for both a new stadium and hospital, ‘A’ and ‘B’ can experience net gains of 100 and 120 respectively. This vote trading may be to their mutual advantage and hence we would expect the deal to go through.

Table also shows that when all three trade votes, net gains per individuals are; A (40) B (10) and C (165). Therefore logrolling may enhance Allocative efficiency and provide for collective agreements that are practically not realized.

In this case, vote trading can work to secure the passage of efficient programs that would otherwise be rejected under simple majority voting. For example ‘A’ and ‘B’ may trade votes to secure proposal stadium and hospital.

The above example of logrolling can lead to the passage of both efficient and inefficient policies that would not otherwise be enacted. It is very difficult to give a ruling as to which of those out comes is more likely to happen.

It is observed that logrolling sometimes promote efficiency and in other cases it thwart it. However it is argued that logrolling is a means of protecting minor­ity interests. Buchanan and Tullock observe that the outcome of this vote trading will be Pareto optimal but the distribution of ben­efits will be indeterminate. It all depends on who forms the majority and on relative bargaining strength.